| (1)∵AD=BC=DC, ∴∠CDB=∠CBD, ∵DC∥BA, ∴∠CDB=∠DBA, ∴∠CBA=2∠DBA, ∵DC∥AB,AD=BC, ∴∠A=∠ABC=2∠DBA, ∵DB⊥AD, ∴∠ADB=90°, ∴∠A=
答:∠A=60°. 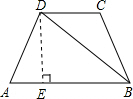 (2)作DE⊥AB于E, ∵∠A=60°,∠DEA=90°, ∴∠ADE=30°, ∴AE=
由勾股定理得:DE=
同理AB=2AC=4cm, ∴梯形ABCD的面积是
答:梯形ABCD的面积是3
|
| (1)∵AD=BC=DC, ∴∠CDB=∠CBD, ∵DC∥BA, ∴∠CDB=∠DBA, ∴∠CBA=2∠DBA, ∵DC∥AB,AD=BC, ∴∠A=∠ABC=2∠DBA, ∵DB⊥AD, ∴∠ADB=90°, ∴∠A=
答:∠A=60°.  (2)作DE⊥AB于E, ∵∠A=60°,∠DEA=90°, ∴∠ADE=30°, ∴AE=
由勾股定理得:DE=
同理AB=2AC=4cm, ∴梯形ABCD的面积是
答:梯形ABCD的面积是3
|
题目简介
如图,在等腰梯形△ABCD中,AB∥CD,AD=BC=CD,BD⊥AD.(1)求∠A的度数.(2)设AD=2cm,求梯形ABCD的面积.-数学
题目详情
(1)求∠A的度数.
(2)设AD=2cm,求梯形ABCD的面积.