如图，CD∥AB，∠ABC，∠BCD的角平分线交于E点，且E在AD上，CE交BA的延长线于F点．（1）BE与CF互相垂直吗？若垂直，请说明理由；（2）若CD=3，AB=4，求BC的长．-数学

题目简介

如图，CD∥AB，∠ABC，∠BCD的角平分线交于E点，且E在AD上，CE交BA的延长线于F点．
（1）BE与CF互相垂直吗？若垂直，请说明理由；
（2）若CD=3，AB=4，求BC的长． 360优课网

题型：解答题难度：中档来源：不详

（1）垂直．
∵CD∥AB，
∴∠ABC+∠BCD=180°，
∵∠ABC，∠BCD的角平分线交于E点，
∴∠ABE=∠EBC，∠DCE=∠ECB，
∴∠EBC+∠ECB=class="stub"1

∠ABC+class="stub"1

∠BCD=class="stub"1

（∠ABC+∠BCD）=90°，
∴∠CEB=90°，
∴BE与CF互相垂直．

（2）∵∠CEB=90°，
∴∠FEB=90°，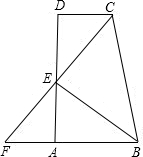
360优课网

在△FBE和△CBE中，
∵

∠CBE=∠FBE

BE=BE

∠BEC=∠BEF

，
∴△FBE≌△CBE（ASA），
∴BF=BC，EF=EC，
∵CD∥AB，
∴∠DCE=∠AFE，
∵∠FEA=∠CED，
∴△DCE≌△AFE，
∴DC=AF，
∵CD=3，AB=4，BF=AF+AB，
∴BF=BC=7．