 (1)证明:∵D、E分别是线段VB,VC的中点,∴DE∥BC ∵DE?平面ABC,BC?平面ABC∴DE∥平面ABC (2)证明:∵VA⊥平面ABC,∴VA⊥BC ∵AB是圆O的直径,点C是圆O上的点,∴∠ACB=90°,∴BC⊥AC ∵VA∩AC=A,∴BC⊥平面VAC,又∵BC?平面VBC, ∴平面VAC⊥平面VBC. |
 (1)证明:∵D、E分别是线段VB,VC的中点,∴DE∥BC ∵DE?平面ABC,BC?平面ABC∴DE∥平面ABC (2)证明:∵VA⊥平面ABC,∴VA⊥BC ∵AB是圆O的直径,点C是圆O上的点,∴∠ACB=90°,∴BC⊥AC ∵VA∩AC=A,∴BC⊥平面VAC,又∵BC?平面VBC, ∴平面VAC⊥平面VBC. |
题目简介
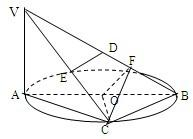
如图,AB是圆O的直径,点C是圆O上的动点,过点A的直线VA垂直于圆O所在的平面ABC,VB与平面ABC成30°的角,D,E分别是线段VB,VC的中点.(1)求证:DE∥平面ABC;(2)求证:平面V
题目详情
(1)求证:DE∥平面ABC;
(2)求证:平面VAC⊥平面VBC.