| (1)证明:∵AD∥BC, ∴∠BAD+∠ABC=180°, ∵∠ABC=90°, ∴∠BAD=∠ABC=90°, ∵DE⊥EC, ∴∠AED+∠BEC=90° ∵∠AED+∠ADE=90°, ∴∠BEC=∠ADE, ∵∠DAE=∠EBC,AE=BC, ∴△EAD≌△EBC, ∴AD=BE. (2)答:△ABF是等腰直角三角形. 理由是:延长AF交BC的延长线于M, 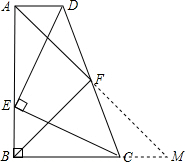 ∵AD∥BM, ∴∠DAF=∠M, ∵∠AFD=∠CFM,DF=FC, ∴△ADF≌△MFC, ∴AD=CM, ∵AD=BE, ∴BE=CM, ∵AE=BC, ∴AB=BM, ∴△ABM是等腰直角三角形, ∵△ADF≌△MCF, ∴AF=FM, ∴∠ABC=90°, ∴BF⊥AM,BF=
∴△AFB是等腰直角三角形. |
题目简介
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.(1)求证:AD=BE;(2)试判断△ABF的形状,并说明理由.-数
题目详情
(1)求证:AD=BE;
(2)试判断△ABF的形状,并说明理由.