 (1)证明:连接OB, ∵GH⊥AB, ∴
∴∠AOG=∠GOB=
∵∠ACB=
∴∠AOG=∠ACB. ∴∠AOD=∠DCE. 又∠ADO=∠CDE, ∴∠OAD=∠E. (2)连接OC,则∠OAD=∠OCA, ∵∠OAD=∠E, ∴∠OCD=∠E. ∵∠DOC=∠COE, ∴△OCD∽△OEC. ∴
∴OC2=OE?OD=(1+3)×1=4. ∴OC=2. 即⊙O的半径为2. (3)当
当
当
|
 (1)证明:连接OB, ∵GH⊥AB, ∴
∴∠AOG=∠GOB=
∵∠ACB=
∴∠AOG=∠ACB. ∴∠AOD=∠DCE. 又∠ADO=∠CDE, ∴∠OAD=∠E. (2)连接OC,则∠OAD=∠OCA, ∵∠OAD=∠E, ∴∠OCD=∠E. ∵∠DOC=∠COE, ∴△OCD∽△OEC. ∴
∴OC2=OE?OD=(1+3)×1=4. ∴OC=2. 即⊙O的半径为2. (3)当
当
当
|
题目简介
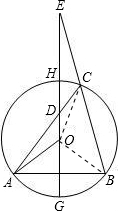
如图,△ABC是⊙O的内接三角形,直径GH⊥AB,交AC于D,GH,BC的延长线相交于E.(1)求证:∠OAD=∠E;(2)若OD=1,DE=3,试求⊙O的半径;(3)当AGB是什么类型的弧时,△CE
题目详情
(1)求证:∠OAD=∠E;
(2)若OD=1,DE=3,试求⊙O的半径;
(3)当