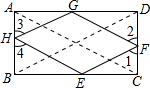
 ∵∠1=∠2=∠3=∠4, ∴∠GHE=∠GFE,∠HGF=∠HEF, 在四边形GHEF中,∠GHE+∠HGF=180°,∠GHE+∠HEF=180°, 故可得HG∥EF,GF∥HE,HGFE是平行四边形, ∴△AHG≌△CFE,△DGF≌△BEH,△BEH∽△CEF,△DGF∽△CEF, ∴
∴EF∥BD, 同理HG∥BD, ∴
∴
又∵
即GF+HG=AC=2, ∴四边形EFGH的周长=2(GF+HG)=4. 故选B. |
 ∵∠1=∠2=∠3=∠4, ∴∠GHE=∠GFE,∠HGF=∠HEF, 在四边形GHEF中,∠GHE+∠HGF=180°,∠GHE+∠HEF=180°, 故可得HG∥EF,GF∥HE,HGFE是平行四边形, ∴△AHG≌△CFE,△DGF≌△BEH,△BEH∽△CEF,△DGF∽△CEF, ∴
∴EF∥BD, 同理HG∥BD, ∴
∴
又∵
即GF+HG=AC=2, ∴四边形EFGH的周长=2(GF+HG)=4. 故选B. |
题目简介
如图,在矩形ABCD中,对角线长2,且∠1=∠2=∠3=∠4,则四边形EFGH的周长为()A.22B.4C.42D.6-数学
题目详情