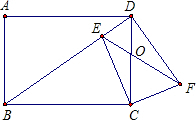
 证明:(1)∵过点C作CF⊥CE交EF于F, ∴∠ECF=90°, ∵∠CEF=∠CBD,∠BCD=90°, ∴△BCD∽△ECF, ∴
(2)设EF和CD的交点为O, ∵△BCD∽△ECF, ∴∠BDC=∠EFC, ∵∠DOE=∠COF, ∴△DOE∽△COF, ∴
∴
∵∠DOF=∠EOC, ∴△ECO∽△DOF, ∴∠CFO=∠CDF, ∴∠EDC+∠CDF=∠BDC+∠DBC=90°, ∴∠BDF=90°, ∴BD⊥DF. |
 证明:(1)∵过点C作CF⊥CE交EF于F, ∴∠ECF=90°, ∵∠CEF=∠CBD,∠BCD=90°, ∴△BCD∽△ECF, ∴
(2)设EF和CD的交点为O, ∵△BCD∽△ECF, ∴∠BDC=∠EFC, ∵∠DOE=∠COF, ∴△DOE∽△COF, ∴
∴
∵∠DOF=∠EOC, ∴△ECO∽△DOF, ∴∠CFO=∠CDF, ∴∠EDC+∠CDF=∠BDC+∠DBC=90°, ∴∠BDF=90°, ∴BD⊥DF. |
题目简介
如图,在矩形ABCD中,点E对角线是BD上一点,作∠CEF=∠CBD,过点C作CF⊥CE交EF于F,连接DF.求证:(1)CECB=CFCD;(2)BD⊥DF.-数学
题目详情
(1)
(2)BD⊥DF.