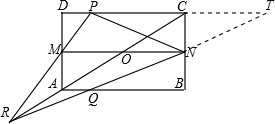
 证明:延长RN交DC于T,连接RC交MN于O, ∵∠BNQ=∠CNT,BN=CN,∠NBQ=∠NCT, ∴△BNQ≌△CNT(ASA), ∴CT=BQ=CP, ∴PN=NT,PC=CT, ∵MN∥CD, ∴MO=ON ∴O是MN的中点所以R,C,O三点共线, 又A,O,C三点共线,所以R,A,C三点共线. |
 证明:延长RN交DC于T,连接RC交MN于O, ∵∠BNQ=∠CNT,BN=CN,∠NBQ=∠NCT, ∴△BNQ≌△CNT(ASA), ∴CT=BQ=CP, ∴PN=NT,PC=CT, ∵MN∥CD, ∴MO=ON ∴O是MN的中点所以R,C,O三点共线, 又A,O,C三点共线,所以R,A,C三点共线. |
题目简介
已知四边形ABCD是矩形,M、N分别是AD、BC的中点,P是CD上一点,Q是AB上一点,CP=BQ,PM与QN的交点为R.求证:R,A,C三点共线.-数学
题目详情