 证明:(1)如图1 ∵∠MAN=120°,AC平分∠MAN, ∴∠DAC=∠BAC=60°, ∵∠ABC=∠ADC=90°, ∴∠DCA=∠BCA=30°, ∵在Rt△ACD中,∠DCA=30°,Rt△ACB中,∠BCA=30°, ∴AC=2AD,AC=2AB, ∴AD+AB=AC. (2)判断是:(1)中的结论①DC=BC;②AD+AB=AC都成立. 理由如下: 如下图,在AN上截取AE=AC,连接CE, ∵∠BAC=60°, ∴△CAE为等边三角形, ∴AC=CE,∠AEC=60°, ∵∠DAC=60°, ∴∠DAC=∠AEC ∵∠ABC+∠ADC=180°,∠ABC+∠EBC=180°, ∴∠ADC=∠EBC, ∴△ADC≌△EBC, ∴DC=BC,DA=BE, ∴AD+AB=AB+BE=AE, ∴AD+AB=AC. |
题目简介
(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:①DC=BC;②AD+AB=AC.请你证明结论②;(2)在图2中,把(1)中的条件“∠ABC=
题目详情
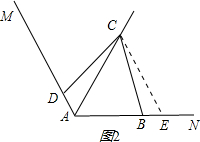
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.