如图，PA为⊙O的切线，B、D为⊙O上的两点，如果∠APB=60°，∠ADB=60°．（1）试判断直线PB与⊙O的位置关系，并说明理由；（2）如果D点是优弧AB上的一个动点，当PA=63且四边形ADB

题目简介

题目详情

如图，PA为⊙O的切线，B、D为⊙O上的两点，如果∠APB=60°，∠ADB=60°．
（1）试判断直线PB与⊙O的位置关系，并说明理由；
（2）如果D点是优弧AB上的一个动点，当PA=6

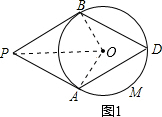
且四边形ADBP是菱形时，求扇形OAMD的面积． 360优课网

题型：解答题难度：中档来源：不详

答案

（1）直线PB与⊙O相切．理由如下：
如图1，连接OP、OB、OA．
∵∠ABD=60°，
∴∠AOB=2∠ADB=120°．
又∵∠APB=60°，
∴∠APB+∠AOB=180°，
∴点P、B、O、A四点共圆，
∴∠PBO+∠PAO=180°．
∵PA为⊙O的切线，
∴∠PAO=90°，
∴∠PBO=90°，即OB⊥PB．
又∵OB是⊙O的半径，
∴直线PB与⊙O相切；

（2）如图2，连接AB、PD、OA．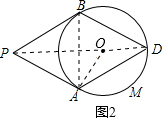
∵
360优课网

四边形ADBP是菱形，
∴PD⊥AB，
∴由垂径定理知，直线PD经过圆心O，
∴∠DPA=class="stub"1

∠BPA=30°．
又∵∠PAO=90°，PA=6

，
∴∠DOA=120°，OA=PA?tan∠DPA=6

=6，
∴S扇形OAMD=

120π×OA2

360

=class="stub"120π×36

360

=12π；

上一篇 : 青海玉树县地震后，吉林电视台法
下一篇 : 如图，在菱形ABCD中，对角线AC与BD

如图，PA为⊙O的切线，B、D为⊙O上的两点，如果∠APB=60°，∠ADB=60°．（1）试判断直线PB与⊙O的位置关系，并说明理由；（2）如果D点是优弧AB上的一个动点，当PA=63且四边形ADB

题目简介

题目详情

答案

更多内容推荐