| 证明:(1)如图,取EC中点F,连接DF. ∵EC⊥平面ABC,BD∥CE,得DB⊥平面ABC. 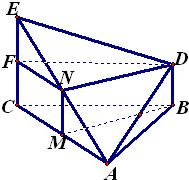 ∴DB⊥AB,EC⊥BC. ∵BD∥CE,BD=
∴DF⊥EC. 又BA=BC=DF, ∴Rt△DEF≌Rt△ABD,所以DE=DA. (2)取AC中点M,连接MN、MB,∵N是EA的中点, ∴MN=
MNBD是矩形,于是DN∥BM. ∵DE=DA,N是EA的中点,∴DN⊥EA.又EA∩MN=M, ∴DN⊥平面ECA,而DN?平面BDN,则平面ECA⊥平面BDN. (3)∵DN⊥平面ECA,DN?平面DEA, ∴平面DEA⊥平面ECA. |
题目简介
如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,CE=CA=2BD,N是EA的中点,求证:(1)DE=DA;(2)平面BDN⊥平面ECA;(3)平面DEA⊥平面ECA.-数学
题目详情
(1)DE=DA;
(2)平面BDN⊥平面ECA;
(3)平面DEA⊥平面ECA.