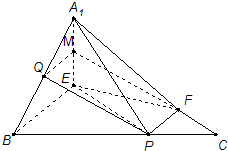
 证明:(Ⅰ)取A1E中点M,连接QM,MF. 在△A1BE中,Q,M分别为A1B,A1E的中点, 所以QM∥BE,且QM=
因为
所以PF∥BE,且PF=
所以QM∥PF,且QM=PF. 所以四边形PQMF为平行四边形. 所以PQ∥FM. …(5分) 又因为FM?平面A1EF,且PQ?平面A1EF, 所以PQ∥平面A1EF. …(7分) 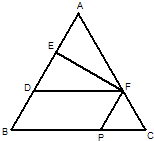 (Ⅱ) 取BE中点D,连接DF. 因为AE=CF=1,DE=1, 所以AF=AD=2,而∠A=60°,即△ADF是正三角形. 又因为AE=ED=1,所以EF⊥AD. 所以在图2中有A1E⊥EF.…(9分) 因为平面A1EF⊥平面EFB,平面A1EF∩平面EFB=EF, 所以A1E⊥平面BEF.…(12分) 又EP?平面BEF, 所以A1E⊥EP.…(14分) |
题目简介
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图
题目详情
(Ⅰ)若Q为A1B中点,求证:PQ∥平面A1EF;
(Ⅱ)求证:A1E⊥EP.