| (1)∵AB=CD,AD=DC, ∴BA=AD,∠BAE=∠ADF, ∵DE=CF, ∴AE=DF, ∴△BAE≌△ADF(SAS). ∴BE=AF.(3分) (2)猜测∠BPF=120°.(1分) ∵由(1)△BAE≌△ADF, ∴∠ABE=∠DAF. ∴∠BPF=∠ABE+∠BAP=∠DAF+∠BAP=∠BAE. 而AD∥BC,∠DCB=∠ABC=60°, ∴∠BPF=120°.(3分) 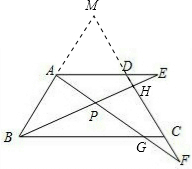 (3)延长BA,CD交于点M,则△MBC为正三角形. ∵∠BPF=120°, ∴∠APB=∠M=60°. 而∠ABP=∠HBM, ∴△ABP∽△HBM. ∴
∴HB=
则S△MBP:S△MBH=BP:BH=81:128.(5分) |
题目简介
如图,在等腰梯形ABCD中,∠DCB=60°,AD∥BC,且AD=DC.E,F分别在AD,DC的延长线上,且DE=CF、AF,BE交于点P,且分别交DC,BC于点H,G.(1)求证:AF=BE;(2)
题目详情
F,BE交于点P,且分别交DC,BC于点H,G.
(1)求证:AF=BE;
(2)请你猜测∠BPF的度数,并证明你的结论;
(3)延长BA,CD相交于M,若AD=24,BP=27,试求三角形MBP和三角形MBH的面积比.