| 图1:∠AMF=∠ENB; 图2:∠AMF=∠ENB; 图3:∠AMF+∠ENB=180°. 证明:如图2,取AC的中点H,连接HE、HF. ∵F是DC的中点,H是AC的中点, ∴HF∥AD,HF=
∴∠AMF=∠HFE, 同理,HE∥CB,HE=
∴∠ENB=∠HEF. ∵AD=BC, ∴HF=HE, ∴∠HEF=∠HFE, 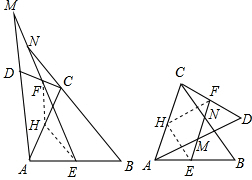 ∴∠ENB=∠AMF. 如图3:取AC的中点H,连接HE、HF. ∵F是DC的中点,H是AC的中点, ∴HF∥AD,HF=
∴∠AMF+∠HFE=180°, 同理,HE∥CB,HE=
∴∠ENB=∠HEF. ∵AD=BC, ∴HF=HE, ∴∠HEF=∠HFE, ∴∠AMF+∠ENB=180°. |
题目简介
已知:在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连接DC.过AB、DC的中点E、F作直线,直线EF与直线AD、BC分别相交于点M、N.(1)如图1,当点D旋转到BC的
题目详情
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连接HE、HF,根据三角形中位线定理和平行线的性质,可得结论∠AMF=∠BNE(不需证明);
(2)当点D旋转到图2或图3中的位置时,∠AMF与
∠BNE有何数量关系?请分别写出猜想,并任选一种情况证明.