 证明:∵O是AC的中点, ∴AO=CO, 又∵在矩形ABCD中,AD∥BC, ∴∠1=∠2 ∴在△AOE和△COF中,
∴△AOE≌△COF(ASA), ∴AE=CF, 又∵EF是AC的垂直平分线, ∴AE=CE,AF=CF, ∴AE=CE=AF=CF, ∴四边形AECF是菱形. |
 证明:∵O是AC的中点, ∴AO=CO, 又∵在矩形ABCD中,AD∥BC, ∴∠1=∠2 ∴在△AOE和△COF中,
∴△AOE≌△COF(ASA), ∴AE=CF, 又∵EF是AC的垂直平分线, ∴AE=CE,AF=CF, ∴AE=CE=AF=CF, ∴四边形AECF是菱形. |
题目简介
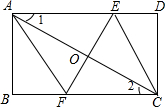
在矩形ABCD中,O是对角线AC的中点,EF是线段AC的中垂线,交AD、BC于E、F.求证:四边形AECF是菱形.-数学
题目详情
求证:四边形AECF是菱形.