| (1)连接EF,FD; ∵GF为圆的切线且又和EB垂直, ∴BE∥FD, ∴∠BEF=∠DFE; 又∵∠DFE=∠FEC, ∴∠BEF=∠CEF, ∴EF为∠BEC的平分线; ∵∠EFC=90°, ∴EF⊥BC, ∴BE=CE ∴△BEC为等腰三角形, ∴BF为BC的一半; ∵ED∥BF, ∴四边形BEDF为平行四边形, 即ED=BF=2.5; 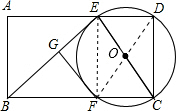 (2)BE不能与⊙O相切. ∵若BE与圆相切, ∴BE⊥EC; ∴△BEC是圆内接三角形,即BC为直径,EF为一个半径, ∵最短为3>2.5, ∴BE不能与⊙O相切. |
题目简介
如图,矩形ABCD中,AB=3,AD=5.点E是AD上的动点,以CE为直径的⊙O与BC交于点F,过点F作FG⊥BE于点G.(1)若FG是⊙O的切线,求DE的长度;(2)试探究:BE能否与⊙O相切?若能
题目详情
(1)若FG是⊙O的切线,求DE的长度;
(2)试探究:BE能否与⊙O相切?若能,求出此时DE的长度;若不能,请说明理由.