| (1)∵PQ⊥AB, ∴∠EQB=∠C=90°, ∴∠BEQ+∠EBQ=90°,∠CBD+∠PDE=90°, ∵BD为∠ABC的平分线, ∴∠CBD=∠EBQ, ∵∠PED=∠BEQ, ∴∠PDE=∠PED; (2)当P在线段AC上时,如图1所示,此时PF∥BD, 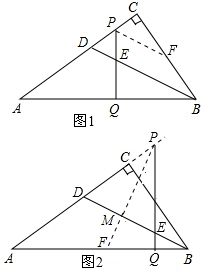 理由为:∵∠PDE=∠PED, ∴PD=PE, ∵PF为∠CPQ的平分线,∠CPQ为△PDE的外角, ∴∠CPF=∠QPF=∠PDE=∠PED, ∴PF∥BD; 当P在线段AC延长线上时,如图2所示,PF⊥BD, 理由为:∵∠PDE=∠PED, ∴PD=PE, ∵PM为∠CPQ的平分线, ∴PF⊥BD. |
题目简介
在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点(不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交直线BD于E.(1)如图①,当点P在线段AC上时,说明∠PD
题目详情
(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)作∠CPQ的角平分线交直线AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.