 假设:OC∥AD. 证明:连接AD、BD. ∵AB是⊙O的直径,CD、CB为⊙O的切线, ∴∠OBC=∠ODC=90°; 又∵OB=OD,OC=OC(公共边), ∴△OBC≌△ODC(HL), ∴∠COD=∠COB(两三角形全等,对应角相等); ∵OA=OD, ∴∠OAD=∠ODA(等边对等角); 又∵∠BOD=∠OAD+∠ODA, ∴∠COD=∠ODA, ∴OC∥AD(内错角相等,两直线平行). |
 假设:OC∥AD. 证明:连接AD、BD. ∵AB是⊙O的直径,CD、CB为⊙O的切线, ∴∠OBC=∠ODC=90°; 又∵OB=OD,OC=OC(公共边), ∴△OBC≌△ODC(HL), ∴∠COD=∠COB(两三角形全等,对应角相等); ∵OA=OD, ∴∠OAD=∠ODA(等边对等角); 又∵∠BOD=∠OAD+∠ODA, ∴∠COD=∠ODA, ∴OC∥AD(内错角相等,两直线平行). |
题目简介
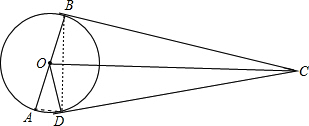
CD、CB为⊙O的切线,B、D为切点,AB是⊙O的直径,试问OC与AD有怎样的位置关系?并证明你的结论.-数学
题目详情