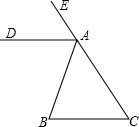
 已知:如图所示,△ABC中,AB=AC,AD为∠EAB的角平分线,求证:AD∥BC. 证明:∵AB=AC,AD为∠EAB的角平分线; ∴∠B=∠C,∠EAD=∠DAB; ∵∠B+∠C+∠BAC=180°, ∠EAD+∠DAB+∠BAC=180°, ∴∠B+∠C=∠EAD+∠DAB; ∴∠B=∠DAB; ∴AD∥CB. |
 已知:如图所示,△ABC中,AB=AC,AD为∠EAB的角平分线,求证:AD∥BC. 证明:∵AB=AC,AD为∠EAB的角平分线; ∴∠B=∠C,∠EAD=∠DAB; ∵∠B+∠C+∠BAC=180°, ∠EAD+∠DAB+∠BAC=180°, ∴∠B+∠C=∠EAD+∠DAB; ∴∠B=∠DAB; ∴AD∥CB. |
题目简介
求证:等腰三角形顶角的外角平分线平行于底边.(要求:画出图形,写出已知、求证,并进行证明)证明:-数学
题目详情
(要求:画出图形,写出已知、求证,并进行证明)
证明: