已知空间四边形OABC,其对角线OB、AC,M、N分别是边OA、CB的中点,点G在线段MN上,且使MG=2GN,用向量OA,OB,OC表示向量OG是()A.OG=OA+23OB+23OCB.OG=12
已知空间四边形OABC,其对角线OB、AC,M、N分别是边OA、CB的中点,点G在线段MN上,且使MG=2GN,用向量表示向量是( )
A.
B.
题目简介
已知空间四边形OABC,其对角线OB、AC,M、N分别是边OA、CB的中点,点G在线段MN上,且使MG=2GN,用向量OA,OB,OC表示向量OG是()A.OG=OA+23OB+23OCB.OG=12
题目详情
已知空间四边形OABC,其对角线OB、AC,M、N分别是边OA、CB的中点,点G在线段MN上,且使MG=2GN,用向量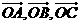 表示向量
表示向量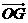 是( )
是( )
A.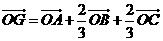
B.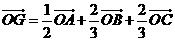
答案