 证明:(1)连接AC,在菱形ABCD中,AC⊥BD, ∵平面ADEF⊥平面ABCD,交线为AD,AE⊥AD,AE?平面ADEF, ∴AE⊥平面ABCD, ∵BD?平面ABCD, ∴AE⊥BD, ∵AC∩AE=A,∴BD⊥平面AEC, ∴BD⊥CE. (2)取AE的中点G,连接PG,QG, 在△ABE中,BP=PE,AG=GE,∴PG∥BA, ∵PG?平面ABCD,BA?平面ABCD, ∴PG∥平面ABCD, 在梯形ADEF中,DQ=QF,AG=GE, ∴GQ∥AD,同理,GQ∥平面ABCD, ∵PG∩GQ=G,PG?平面PGQ,GQ?PQG, ∴平面PQG∥平面ABCD, ∵PQ?平面PQG, ∴PQ∥平面ABCD. |
题目简介
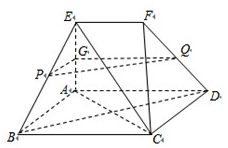
如图,空间几何体ABCDEF中,四边形ABCD是菱形,直角梯形ADFE所在平面与面ABCD垂直,且AE⊥AD,EF∥AD,其中P,Q分别为棱BE,DF的中点.(1)求证:BD⊥CE;(2)求证:PQ∥
题目详情
(1)求证:BD⊥CE;
(2)求证:PQ∥平面ABCD.