 (Ⅰ)∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB BC?平面ABCD,而四边形ABCD为矩形∴BC⊥AB, ∴BC⊥平面ABEF∵AF?平面ABEF∴BC⊥AF ∵BF⊥AF,BC∩BF=B∴AF⊥平面FBC; (Ⅱ)取FD中点N,连接MN、AN,则MN∥CD,且MN=
又四边形ABCD为矩形,∴MN∥OA,且MN=OA ∴四边形AOMN为平行四边形,∴OM∥AN 又∵OM?平面DAF,AN?平面DAF∴OM∥平面DAF. |
 (Ⅰ)∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB BC?平面ABCD,而四边形ABCD为矩形∴BC⊥AB, ∴BC⊥平面ABEF∵AF?平面ABEF∴BC⊥AF ∵BF⊥AF,BC∩BF=B∴AF⊥平面FBC; (Ⅱ)取FD中点N,连接MN、AN,则MN∥CD,且MN=
又四边形ABCD为矩形,∴MN∥OA,且MN=OA ∴四边形AOMN为平行四边形,∴OM∥AN 又∵OM?平面DAF,AN?平面DAF∴OM∥平面DAF. |
题目简介
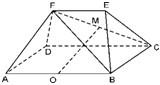
已知多面体ABCDFE中,四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD,O、M分别为AB、FC的中点,且AB=2,AD=EF=1.(Ⅰ)求证:AF⊥平面FBC;(Ⅱ)求证:
题目详情
(Ⅰ)求证:AF⊥平面FBC;
(Ⅱ)求证:OM∥平面DAF.