 (1)证明:连接AF, ∵在矩形ABCD中,AD=4,AB=2,F是线段BC的中点, ∴FC=CD,∴△FCD是等腰直角三角形, ∴∠DFC=45°,同理可得∠AFB=45°, ∴AF⊥FD. 又∵PA⊥面ABCD,∴PA⊥FD,∵AF∩PA=A ∴FD⊥平面PAF,∴PF⊥FD.(6分) (2)在AP上存在点G, 且AG=
证明:取AD中点I,取AI中点H,连接BI,EH,EG,GH, ∵DI
∴BI∥FD 又∵E、H分别是AB、AI的中点, ∴EH∥BI,∴EH∥FD 而EH?平面PFD,∴EH∥平面PFD∵
∴GH∥PD 而GH?平面PFD, ∴HG∥平面PFD 又∵EH∩GH=H ∴平面EHG∥平面PFD ∴EG∥平面PFD 从而G为所求. |
题目简介
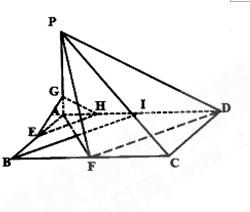
已知ABCD是矩形,AD=4,AB=2,E、F分别是线段AB、BC的中点,PA⊥面ABCD.(1)证明:PF⊥FD;(2)在PA上是否存在点G,使得EG∥平面PFD.-数学
题目详情
(1)证明:PF⊥FD;
(2)在PA上是否存在点G,使得EG∥平面PFD.