 (1)连接CG交AP于M点,连接BM. ∵
∴FG∥BM, 又BM?平面PAB,FG?平面PAB ∴FG∥平面PAB. (2)∵PA⊥平面ABCD, ∴PA⊥AC, 又∵AC⊥AB,PA∩AB=A. ∴AC⊥平面PAB,∴AC⊥BM, ∵FG∥BM,∴FG⊥AC. (3)连结EM,由(2)知FG⊥AC,若FG⊥平面ACE, 则FG⊥AE,即BM⊥AE,又EM=
设EA∩BM=H,则EH=
设PA=a,则EA=
因为Rt△AME~Rt△MHE, 所以EM2=EH?EA, 即1=
即PA=2
|
 (1)连接CG交AP于M点,连接BM. ∵
∴FG∥BM, 又BM?平面PAB,FG?平面PAB ∴FG∥平面PAB. (2)∵PA⊥平面ABCD, ∴PA⊥AC, 又∵AC⊥AB,PA∩AB=A. ∴AC⊥平面PAB,∴AC⊥BM, ∵FG∥BM,∴FG⊥AC. (3)连结EM,由(2)知FG⊥AC,若FG⊥平面ACE, 则FG⊥AE,即BM⊥AE,又EM=
设EA∩BM=H,则EH=
设PA=a,则EA=
因为Rt△AME~Rt△MHE, 所以EM2=EH?EA, 即1=
即PA=2
|
题目简介
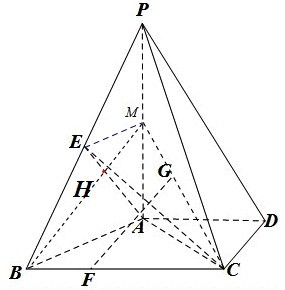
如图所示,PA⊥平面ABCD,∠ADC=90°,AD∥BC,AB⊥AC,且AB=AC=2,G为△PAC的重心,E为PB的中点,F在线段BC上,且CF=2FB.(1)求证:FG∥平面PAB;(2)求证:
题目详情
(1)求证:FG∥平面PAB;
(2)求证:FG⊥AC;
(3)当PA长度为多少时,FG⊥平面ACE?