 证明:(Ⅰ)取CE中点P,连接FP、BP, ∵F为CD的中点, ∴FP∥DE,且FP=
又AB∥DE,且AB=
∴AB∥FP,且AB=FP, ∴ABPF为平行四边形,∴AF∥BP.(4分) 又∵AF?平面BCE,BP?平面BCE, ∴AF∥平面BCE(6分) (Ⅱ)∵△ACD为正三角形,∴AF⊥CD ∵AB⊥平面ACD,DE∥AB ∴DE⊥平面ACD又AF?平面ACD ∴DE⊥AF 又AF⊥CD,CD∩DE=D ∴AF⊥平面CDE(10分) 又BP∥AF∴BP⊥平面CDE 又∵BP?平面BCE ∴平面BCE⊥平面CDE(12分) |
题目简介
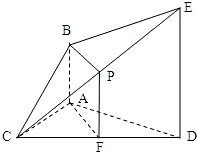
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.(Ⅰ)求证:AF∥平面BCE;(Ⅱ)求证:平面BCE⊥平面CDE.-数学
题目详情
(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE.