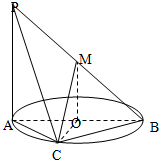
 由题意可知PA⊥平面ABC,点M为线段PB的中点,O是圆的圆心,所以MO⊥平面ABC,PA∥OM,所以PA与MO共面,(1)不正确; 又PA∥OM,OM?平面PAC,PA?平面PAC,∴MO∥平面PAC;(2)正确; 因为AB为圆O的直径,点C在圆周上(异于A,B点),所以OC不垂直AC,所以OC⊥平面PAB;不正确; 因为AB为圆O的直径,点C在圆周上(异于A,B点),所以BC⊥AC,∵直线PA垂直于圆所在的平面,∴BC⊥PA,可知BC⊥平面PAC,BC?平面PBC,所以平面PAC⊥平面PBC, (4)正确. 故答案为:(2)(4). |
题目简介
如图AB为圆O的直径,点C在圆周上(异于A,B点)直线PA垂直于圆所在的平面,点M为线段PB的中点,有以下四个命题:(1)PA∥平面MOB;(2)MO∥平面PAC;(3)OC⊥平面PAB;(4)平面P
题目详情
(1)PA∥平面MOB; (2)MO∥平面PAC;
(3)OC⊥平面PAB; (4)平面PAC⊥平面PBC,
其中正确的命题是______.