 证明:(1)因为AD=2BC,且O是AD中点, 所以OD=BC,又AD∥BC,所以OD∥BC, 所以四边形BCDO为平行四边形,(2分) 所以CD∥BO,CD?平面PBO, 且BO?平面PBO,故CD∥平面PBO;(6分) (2)因为∠BAD=90°,所以BA⊥AD, 又平面PAD⊥平面ABCD, 且平面PAD∩平面ABCD=AD,AB?平面ABCD, ∴AB⊥平面PAD,(8分)PD?平面PAD, ∴AB⊥PD,AP⊥PD,AB∩AP=A, ∴PD⊥平面PAB,(12分)∵PD?平面PCD, 故平面PAB⊥平面PCD. (14分) |
题目简介
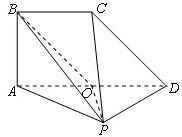
如图,平面ABCD⊥平面PAD,△APD是直角三角形,∠APD=90°,四边形ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=2BC,O是AD的中点(1)求证:CD∥平面PBO;(2)求证
题目详情
(1)求证:CD∥平面PBO;
(2)求证:平面PAB⊥平面PCD.