| (1)证明:由题意可知,△PAC为等腰直角三角形,△ABC为等边三角形. 因为O为边AC的中点,所以BO⊥AC, 因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BO?平面ABC,所以,BO⊥面PAC. 因为PA?平面PAC,故 BO⊥PA.在等腰三角形PAC内,O,E为所在边的中点,故 OE∥PC,∴OE⊥PA, 又BO∩OE=O,所以,PA⊥平面EBO. (2)证明:连AF交BE于Q,连QO.因为E、F、O分别为边PA、PB、PC的中点, 所以
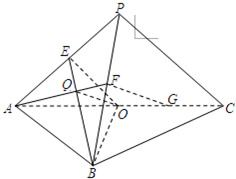 于是,
因为FG?平面EBO,QO?平面EBO,所以,FG∥平面EBO. |
题目简介
如图,平面PAC⊥平面ABC,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=22.求证:(1)PA⊥平面EBO;(2)FG∥平面EBO.-数学
题目详情
求证:(1)PA⊥平面EBO;
(2)FG∥平面EBO.