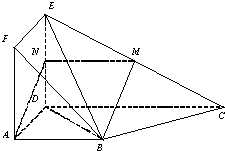
 证明:(I)取DE中点N,连接MN,AN 在△EDC中,M,N分别为EC,ED的中点 ∴MN∥CD,且MN=
由已知中AB∥CD,AB=AD=2,CD=4, ∴MN∥AB,且MN=AB ∴四边形ABMN为平行四边形 ∴BM∥AN 又∵AN?平面ADEF BM?平面ADEF ∴BM∥平面ADEF (II)∵ADEF为正方形 ∴ED⊥AD 又∵正方形ADEF与梯形ABCD所在的平面互相垂直,且ED?平面ADEF ∴ED⊥平面ABCD ∴ED⊥BC 在直角梯形ABCD中,AB=AD=2,CD=4,可得BC=2
在△BCD中,BD=BC=2
∴BC⊥BD ∴BC⊥平面BDE 又∵BC?平面BEC ∴平面BDE⊥平面BEC |
题目简介
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.(I)求证:BM∥平面ADEF;(Ⅱ)求证:平面BDE⊥平面BEC.-数学
题目详情
(I)求证:BM∥平面ADEF;
(Ⅱ)求证:平面BDE⊥平面BEC.