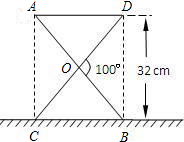
 解法1:连接AC,BD. ∵OA=OB=OC=OD, ∴四边形ACBD为矩形. ∵∠DOB=100°,∴∠ABC=50°. 由已知得AC=32, 在Rt△ABC中,sin∠ABC=
∴AB=
tan∠ABC=
∴BC=
∴AD=BC=26.9(cm). 答:椅腿AB的长为41.8cm,篷布面的宽AD为26.9cm. 解法2:作OE⊥AD于E. ∵OA=OB=OC=OD,∠AOD=∠BOC, 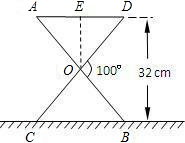 ∴△AOD≌△BOC. ∵∠DOB=100°, ∴∠OAD=50°. ∴OE=
在Rt△AOE中,sin∠OAE=
∴AO=
∴AB=2AO≈41.8(cm). tan∠OAE=
∴AD=2AE≈26.9(cm). 答:椅腿AB的长为41.8cm,篷布面的宽AD为26.9cm. |
题目简介
某大学计划为新生配备如图(1)所示的折叠椅.图(2)是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长相等,O是它们的中点.为使折叠椅既舒适又牢固,厂家将撑开后的折叠椅高度设-数学
题目详情