 (1)证明:①∵∠BAC=90°, AB=AC=6,D为BC中点 ∴∠BAD=∠DAC=∠B=∠C=45°, ∴AD=BD=DC, ∵在△AED和△CFD中,
∴△AED≌△CFD(SAS); ②∵△AED≌△CFD, ∴DE=DF,∠ADE=∠CDF, 又∵∠CDF+∠ADF=90°, ∴△DEF为等腰直角三角形; (2)△DEF为等腰直角三角形, 理由:∵∠BAC=90° AB=AC=6,D为BC中点 ∴∠BAD=∠DAC=∠B=∠C=45°, ∴AD=BD=DC, ∵在△AED和△CFD中,
∴△AED≌△CFD(SAS); ∴DE=DF∠ADE=∠CDF, 又∵∠CDF+∠ADF=90°, ∴△DEF为等腰直角三角形. |
题目简介
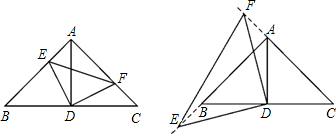
如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点.(1)如图1,若E、F分别是AB、AC上的点,且AE=CF.求证:①△AED≌△CFD;②△DEF为等腰直角三角形.(2)如图2,
题目详情
(1)如图1,若E、F分别是AB、AC上的点,且AE=CF.求证:①△AED≌△CFD;②△DEF为等腰直角三角形.
(2)如图2,点F、E分别D在CA、AB的延长线上,且AE=CF,猜想△DEF是否为等腰直角三角形?如果是请给出证明.