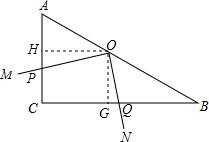
 过点O作OH⊥AC于H,OG⊥BC于G, ∴∠OHP=∠OGQ=90°. ∵∠ACB=90°, ∴四边形HCGO为矩形, ∴∠HOG=90°, ∴∠HOP=∠GOQ, ∴△PHO∽△QGO, ∴
∵
∴AH=
在Rt△AHO中,由勾股定理,得 OH=
∴
∴
故答案为:
|
 过点O作OH⊥AC于H,OG⊥BC于G, ∴∠OHP=∠OGQ=90°. ∵∠ACB=90°, ∴四边形HCGO为矩形, ∴∠HOG=90°, ∴∠HOP=∠GOQ, ∴△PHO∽△QGO, ∴
∵
∴AH=
在Rt△AHO中,由勾股定理,得 OH=
∴
∴
故答案为:
|
题目简介
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,直角∠MON的顶点O在AB上,OM、ON分别交CA、CB于点P、Q,∠MON绕点O任意旋转.当OAOB=12时,OPOQ的值为______.
题目详情