(1)延长DM交EF于H点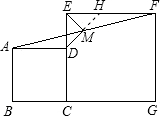 ∵正方形ABCD和正方形CEFG,M为AF的中点, ∴∠DAM=∠HFM,AM=MF,∠AMD=∠FMH. ∴△MAD≌△MFH. ∴DM=MH,AD=FH. ∴ED=EH,△DEH为等腰直角三角形, ∴△MDE为等腰直角三角形; (2)△MDE为等腰直角三角形. 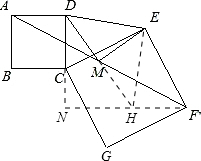 (3)如图,延长DM到H使DM=MH,连接EH,延长FH于DC的延长线交于点N. 易证△ADM≌△FHM,∴AD=FH=CD. ∵∠DCE+∠NCG=90°,∠EFH+∠NFG=90°, ∴∠DCE=∠EFH. ∴△DCE≌△FHE. ∴DE=EH,∠DEC=∠FEH,∠DEH=90°. ∵DM=EM, ∴△MDE为等腰直角三角形. |
题目简介
正方形ABCD和正方形CEFG,M为AF的中点,连接MD、ME.(1)如图,B、C、G依次在同一条直线上,求证:△MDE等腰直角三角形;(2)如图,正方形CEFG绕顶点C旋转45°,使B、C、F依次在
题目详情
(1)如图,B、C、G依次在同一条直线上,求证:△MDE等腰直角三角形;
(2)如图,正方形CEFG绕顶点C旋转45°,使B、C、F依次在同一条直线上,则△MDE的形状是______;
(3)如图,将正方形CEFG任意旋转,设∠DCE=α°,猜想△MDE的形状,写出你的结论并给予证明.