正方形ABCD和正方形AEFG有一公共点A，点G．E分别在线段AD、AB上（如图（1）所示），连接DF、BF．（1）求证：DF=BF，（2）若将正方形AEFG绕点A按顺时针方向旋转，连接DG、BE（如

题目简介

题目详情

正方形ABCD和正方形AEFG有一公共点A，点G．E分别在线段AD、AB上（如图（1）所示），连接DF、BF．
（1）求证：DF=BF，
（2）若将正方形AEFG绕点A按顺时针方向旋转，连接DG、BE（如图（2）
360优课网

所示），在旋转过程中，请猜想线段DG、BE始终有什么数量关系和位置关系并证明你的猜想．

题型：解答题难度：中档来源：鄂州

答案

（1）证明：∵AD=AB，AG=AE=EF=FG，
∠DGF=∠BEF=90°，
∴DG=BE，
∴△DGF≌△BEF，
∴DF=BF．

（2）猜想：DG=BE，DG⊥BE．
证明：如图，由正方形性质与旋转知AD=AB，AG=AE，∠DAG=∠BAE，
∴△DAG≌△BAE，
∴DG=BE，（6分）∠ADG=∠ABE，
延长DG交BE或延长线于H，交AB于I，
∵∠ADG=∠ABE，∠DIA=∠BIH，
又∵∠ADG+∠DIA=90°，
∴∠ABE+∠BIH=90°，
∴∠DHB=90°，
即DG⊥BE．

上一篇 : Did you ever think someone w
下一篇 : 线段AB和CD互相垂直平分于O点，

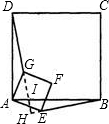
正方形ABCD和正方形AEFG有一公共点A，点G．E分别在线段AD、AB上（如图（1）所示），连接DF、BF．（1）求证：DF=BF，（2）若将正方形AEFG绕点A按顺时针方向旋转，连接DG、BE（如

题目简介

题目详情

答案

更多内容推荐