如图，在△ABC和△DBC中，已知∠ACB=∠DBC=90°，点E为BC的中点，DE⊥AB，垂足为F，且AB=DE．（1）求证：△DBC是等腰Rt△；（2）若BD=8cm，求AC的长；（3）在（2）的

题目简介

如图，在△ABC和△DBC中，已知∠ACB=∠DBC=90°，点E为BC的中点，DE⊥AB，垂足为F，且AB=DE．
（1）求证：△DBC是等腰Rt△；
（2）若BD=8cm，求AC的长；
（3）在（2）的条件下求BF的长． 360优课网

题型：解答题难度：中档来源：不详

（1）证明：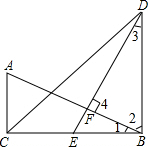

∵DE⊥AB，
∴∠4=90°=∠ACB=∠EBD，
∴∠1+∠2=90°，∠2+∠3=90°，
∴∠1=∠3，
在△ACB和△EBD中，
∵

∠1=∠3

∠ACB=∠EBD

AB=DE

，
∴△ACB≌△EBD（AAS），
∴BC=BD，
∵∠EBD=90°，
∴△CBD是等腰直角三角形；

（2）∵BC=BD=8cm，△ACB≌△EBD，
∴AC=BE，
∵E为BC中点，
∴BE=class="stub"1

BC=4cm，

∴AC=BE=4cm；

（3）在Rt△EBD中，BD=8cm，BE=4cm，由勾股定理得：DE=4

cm，
在△EBD中，S△EBD=class="stub"1

×BE×BD=class="stub"1

×DE×BF，
∴BE×BD=DE×BF，
∴4cm×8cm=4

cm×BF，
∴BF=

cm．