首页 > 在锐角△ABC中，∠BAC=60°，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①DF=EF；②AD：AB=AE：AC；③△DEF是等边三角形；④BE+CD=BC；⑤当∠ABC=45

在锐角△ABC中，∠BAC=60°，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①DF=EF；②AD：AB=AE：AC；③△DEF是等边三角形；④BE+CD=BC；⑤当∠ABC=45

题目简介

在锐角△ABC中，∠BAC=60°，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①DF=EF；②AD：AB=AE：AC；③△DEF是等边三角形；④BE+CD=BC；⑤当∠ABC=45

题目详情

在锐角△ABC中，∠BAC=60°，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①DF=EF；②AD：AB=AE：AC；③△DEF是等边三角形；④BE+CD=BC；⑤当∠ABC=45°时，BE=
2
DE中，一定正确的有______．360优课网
题型：填空题难度：中档来源：不详

答案

①∵BD、CE为高，∴△BEC、△BDC是直角三角形．
∵F是BC的中点，∴EF=DF=class="stub"1
2
BC．故正确；

360优课网
②∵∠ADB=∠AEC=90°，∠A公共，∴△ABD∽△ACE，得AD：AB=AE：AC．故正确；
③∵∠A=60°，∴∠ABC+∠ACB=120°．
∵F是BC的中点，∴EF=BF，DF=CF．∴∠ABF=∠BEF，∠ACB=∠CDF．
∴∠BFE+∠CFD=120°，∠EFD=60°．又∵EF=FD，∴△DEF是等边三角形．故正确；
④若BE+CD=BC，则可在BC上截取BH=BE，则HC=CD．
∵∠A=60°，∴∠ABC+∠ACB=120°．又∵BH=BE，HC=CD，
∴∠BHE+∠CHD=120°，∠EHD=60°．
所以存在满足条件的点，假设成立，但一般情况不一定成立，故错误；
⑤∵∠ABC=45°，∴BE=
2
2
BC=
2
DE．
正确的①②③⑤．
故答案为①②③⑤．

更多内容推荐

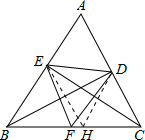
Copyright © 2018-2020 360优课网