| 当P为AB上时,假设P为中点时,AP=PB=PC,满足条件, 当点P不为中点时,过点C作AB的垂线,亦满足条件; 当点P在BA的延长线上时,过点P作PF⊥BC,PE⊥CA; 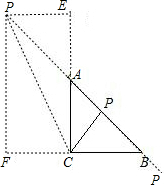 PC2=PF2+CF2,AP2=AE2+PE2=AE2+FC2=2CF2 PB2=BF2+PF2=PF2+(BC+CF)2=2PF2 AP2+PB2=2CF2+PF2+PF2 2PC2=2PF2+2CF2 所以AP2+PB2=2PC2, 即k=2CP2; 同理,当点P在AB的延长线上时,k=2CP2. 综上可知:k=2CP2. 故选D. |
题目简介
点P在等腰Rt△ABC的斜边AB所在直线上,若记:k=AP2+BP2,则()A.满足条件k<2CP2的点P有且只有一个B.B满足条件k<2CP2的点P有无数个C.C满足条件k=2CP2的点P有有限个D
题目详情