如图，∠ABM为直角，点C为线段BA的中点，点D是射线BM上的一个动点（不与点B重合），连接AD，作BE⊥AD，垂足为E，连接CE，过点E作EF⊥CE，交BD于F．（1）求证：BF=FD；（2）∠A在

题目简介

题目详情

如图，∠ABM为直角，点C为线段BA的中点，点D是射线BM上的一个动点（不与点B重合）
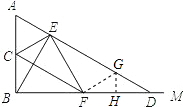
360优课网

，连接AD，作BE⊥AD，垂足为E，连接CE，过点E作EF⊥CE，交BD于F．
（1）求证：BF=FD；
（2）∠A在什么范围内变化时，四边形ACFE是梯形，并说明理由；
（3）∠A在什么范围内变化时，线段DE上存在点G，满足条件DG=

DA，并说明理由．

题型：解答题难度：中档来源：黄石

答案

（1）证明：在Rt△AEB中，
∵AC=BC，
∴CE=class="stub"1

AB，
∴CB=CE，
∴∠CEB=∠CBE．
∵∠CEF=∠CBF=90°，
∴∠BEF=∠EBF，
∴EF=BF．
∵∠BEF+∠FED=90°，∠EBD+∠EDB=90°，
∴∠FED=∠EDF．
∴BF=FD；

（2）由（1）BF=FD，而BC=CA，
∴CF∥AD，即AE∥CF．
若AC∥EF，则AC=EF，
∴BC=BF．∴BA=BD，∠A=45°．
∴0°＜∠A＜90°且∠A≠45°时，四边形ACFE为梯形；

（3）作GH⊥BD，垂足为H，则GH∥AB．
∵DG=class="stub"1

DA，
∴DH=class="stub"1

DB．
又F为BD中点，
∴H为DF的中点．
∴GH为DF的中垂线．
∴∠GDF=∠GFD．
∵点G在ED上，
∴∠EFD≥∠GFD．
∵∠EFD+∠FDE+∠DEF=180°，
∴∠GFD+∠FDE+∠DEF≤180度．
∴3∠EDF≤180度．
∴∠EDF≤60度．
又∠A+∠EDF=90°，
∴30°≤∠A＜90°．
∴当30°≤∠A＜90°时，
DE上存在点G，满足条件DG=class="stub"1

DA．

上一篇 : 在锐角△ABC中，∠BAC=60°，BD、C
下一篇 : （1）血液是由______和血细胞构成

如图，∠ABM为直角，点C为线段BA的中点，点D是射线BM上的一个动点（不与点B重合），连接AD，作BE⊥AD，垂足为E，连接CE，过点E作EF⊥CE，交BD于F．（1）求证：BF=FD；（2）∠A在

题目简介

题目详情

答案

更多内容推荐