证明:作FQ⊥BD于Q,如图,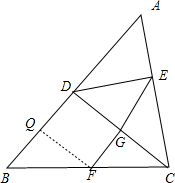 ∴∠FQB=90°, ∵DE⊥AC, ∴∠DEC=90° ∵FG⊥CD CD⊥BD, ∴BD∥FG,∠BDC=∠FGC=90°, ∴四边形DGFQ为矩形, ∴QF=DG, ∴∠B=∠GFC ∵F为BC中点 ∴BF=FC, ∵在Rt△BQF与Rt△FGC中,
∴△BQF≌△FGC(AAS), ∴QF=GC, ∵QF=DG, ∴DG=GC, 在Rt△DEC中, ∵G为DC中点, ∴DG=EG. |
证明:作FQ⊥BD于Q,如图, ∴∠FQB=90°, ∵DE⊥AC, ∴∠DEC=90° ∵FG⊥CD CD⊥BD, ∴BD∥FG,∠BDC=∠FGC=90°, ∴四边形DGFQ为矩形, ∴QF=DG, ∴∠B=∠GFC ∵F为BC中点 ∴BF=FC, ∵在Rt△BQF与Rt△FGC中,
∴△BQF≌△FGC(AAS), ∴QF=GC, ∵QF=DG, ∴DG=GC, 在Rt△DEC中, ∵G为DC中点, ∴DG=EG. |
题目简介
已知△ABC中,CD⊥AB于D,过D作DE⊥AC,F为BC中点,过F作FG⊥DC,求证:DG=EG.-数学
题目详情