 (1)△APB是直角三角形有两种情况: 作直径AP2、BPl,连接PlA、P2B, ∴P2B=AB÷tan∠APB=5, PlB=AP2=5
所以PB的长为5或5
(2)△APB为等腰三角形时有三种情况: ①PA=PB, ∵∠AOH=∠APB,AB=10 ∴OH=
∴S△APB=
②BA=BP, ∴∠GAB=∠APB 在⊙O上取一点P4使BP4=BA,连接AP4交P1B于G 设AG=k ∵tan∠APB=2 ∴BG=2k 由勾股定理得k=2
∴S△APB=40; ③AB=AP与BA=BP情况相同 ∴S△APB=40. |
题目简介
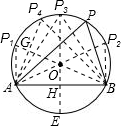
如图,⊙O的弦AB=10,P是弦AB所对优弧上的一个动点,tan∠APB=2,(1)若△APB为直角三角形,求PB的长;(2)若△APB为等腰三角形,求△APB的面积.-数学
题目详情
(1)若△APB为直角三角形,求PB的长;
(2)若△APB为等腰三角形,求△APB的面积.