| (1)证明:由题意可得ABCD是等腰梯形, ∴∠A=∠D, 在△ABE和△DCE中,
∴△ABE≌△DCE. (2)四边形EGFH是菱形. 证明:∵GF、FH是△EBC的中位线,且由(1)得EB=EC, ∴GF∥EH,GE∥HF,GF=GE, ∴四边形EGFH是菱形. (3)EF⊥BC,且EF=
 证明:连接EF, ∵EFGH是正方形, ∴∠GEH=90°,即△BEC是等腰直角三角形 ∴EF⊥BC,且EF=
|
| (1)证明:由题意可得ABCD是等腰梯形, ∴∠A=∠D, 在△ABE和△DCE中,
∴△ABE≌△DCE. (2)四边形EGFH是菱形. 证明:∵GF、FH是△EBC的中位线,且由(1)得EB=EC, ∴GF∥EH,GE∥HF,GF=GE, ∴四边形EGFH是菱形. (3)EF⊥BC,且EF=
 证明:连接EF, ∵EFGH是正方形, ∴∠GEH=90°,即△BEC是等腰直角三角形 ∴EF⊥BC,且EF=
|
题目简介
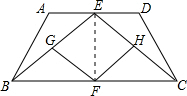
如图,已知:梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是AD、BC、BE、CE的中点.(1)求证:△ABE≌△DCE.(2)四边形EGFH是什么特殊四边形?并证明你的结论.(3)连接E
题目详情
中点.
(1)求证:△ABE≌△DCE.
(2)四边形EGFH是什么特殊四边形?并证明你的结论.
(3)连接EF,当四边形EGFH是正方形时,线段EF与BC有什么关系?请说明理由.