 (1)证明:∵AB是⊙O的直径, ∴∠ACB=90°; ∴∠CAB+∠CBA=90°; 又∠PAC=∠B, ∴∠CAB+∠PAC=90°; ∴∠PAB=90°; 即PA是⊙O的切线. (2)设CE=6x,AE=2y,则DE=5x,BE=3y; 由相交弦定理,得:AE?EB=CE?DE,即: 2y?3y=5x?6x,解得:
∵∠ACD=∠ABD,∠AEC=∠DEB, ∴△AEC∽△DEB,则有:
∵AE=2y=2
∴
设BC=m,同理可求得AD=
∵AB是直径,∴△ACB、△ADB是直角三角形; 由勾股定理,得:AB2=AC2+BC2=AD2+BD2,即: 82+m2=(
故BC=6,AD=2
∴AB=
|
题目简介
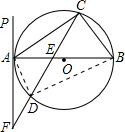
如图,△ABC内接于⊙O,AB是⊙O的直径,PA是过A点的直线,∠PAC=∠B,(1)求证:PA是⊙O的切线;(2)如果弦CD交AB于E,CD的延长线交PA于F,AC=8,CE:ED=6:5,AE:E
题目详情
(1)求证:PA是⊙O的切线;
(2)如果弦CD交AB于E,CD的延长线交PA于F,AC=8,CE:ED=6:5,AE:EB=2:3,求AB的长和∠ECB的正切值.