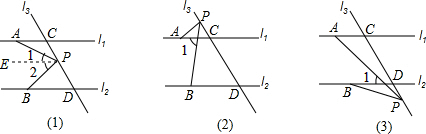 (1)∠APB=∠PAC+∠PBD. 证明:过点P作PE∥l1, ∵l1∥l2, ∴PE∥l1∥l2, ∴∠1=∠PAC,∠2=∠PBD, ∴∠APB=∠1+∠2=∠PAC+∠PBD; (2)∠PAC+∠APB=∠PBD. 证明:∵l1∥l2, ∴∠1=∠PBD, ∵∠1=∠PAC+∠APB, ∴∠PAC+∠APB=∠PBD. (3)∠PBD+∠APB=∠PAC. 证明:∵l1∥l2, ∴∠1=∠PAC, ∵∠1=∠PBD+∠APB, ∴∠PBD+∠APB=∠PAC. |
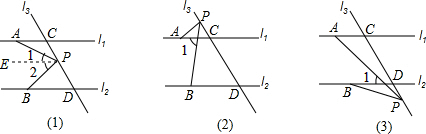 (1)∠APB=∠PAC+∠PBD. 证明:过点P作PE∥l1, ∵l1∥l2, ∴PE∥l1∥l2, ∴∠1=∠PAC,∠2=∠PBD, ∴∠APB=∠1+∠2=∠PAC+∠PBD; (2)∠PAC+∠APB=∠PBD. 证明:∵l1∥l2, ∴∠1=∠PBD, ∵∠1=∠PAC+∠APB, ∴∠PAC+∠APB=∠PBD. (3)∠PBD+∠APB=∠PAC. 证明:∵l1∥l2, ∴∠1=∠PAC, ∵∠1=∠PBD+∠APB, ∴∠PBD+∠APB=∠PAC. |
题目简介
如图,l1∥l2,l3与l1、l2相交于C、D二点,点P在l3上,在图(1)、(2)、(3)中分别探究∠PAC、∠APB、∠PBD三者间关系,并证明.-数学
题目详情