 (1)∵△ABC≌△DCB, ∴∠1=∠2,AB=CD, ∵∠AOB=∠DOC, ∴∠3=∠4, 在△AOB与△DOC中, ∵
∴△AOB≌△DOC, ∴OC=OB; (2)∵△ABC≌△DCB, ∴∠1=∠2,∠3=∠4,OA=OD,OB=OC, ∴∠CAD=∠BDA,∠OBC=∠OCB, ∴∠1+∠CAD=∠2+∠BDA,∠3+∠OBC=∠4+∠OCB,即∠BAD=∠CDA,∠ABC=∠BCD, ∵四边形的内角和是360°, ∴∠BAC+∠ABC=180°, ∴AD∥BC. |
 (1)∵△ABC≌△DCB, ∴∠1=∠2,AB=CD, ∵∠AOB=∠DOC, ∴∠3=∠4, 在△AOB与△DOC中, ∵
∴△AOB≌△DOC, ∴OC=OB; (2)∵△ABC≌△DCB, ∴∠1=∠2,∠3=∠4,OA=OD,OB=OC, ∴∠CAD=∠BDA,∠OBC=∠OCB, ∴∠1+∠CAD=∠2+∠BDA,∠3+∠OBC=∠4+∠OCB,即∠BAD=∠CDA,∠ABC=∠BCD, ∵四边形的内角和是360°, ∴∠BAC+∠ABC=180°, ∴AD∥BC. |
题目简介
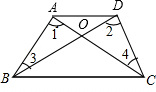
如图,四边形ABCD的对角线AC、BD相交于点O,△ABC≌△DCB.求证:(1)OC=OB(2)AD∥BC.-数学
题目详情
求证:(1)OC=OB
(2)AD∥BC.