如图，正方形ABCD的对角线AC、BD相交于O．（1）（图1）若E为AC上一点，过A作AG⊥EB于G，AG、BD交于F，求证：OE=OF；（2）（图2）若E为AC延长线上一点，AG⊥EB交EB的延长线

题目简介

题目详情

如图，正方形ABCD的对角线AC、BD相交于O．
（1）（图1）若E为AC上一点，过A作AG⊥EB于G，AG、BD交于F，求证：OE=OF；
（2）（图2）若E为AC延长线上一点，AG⊥EB交EB的延长线于G，AG的延长线交DB的延长线于F，其他条件不变，OE=OF还成立吗？若成立，请予以证明；若不成立，请说明理由．

360优课网

题型：解答题难度：中档来源：不详

答案

证明：（1）如图（1）
正方形ABCD中，
∴AO=BO，∠AOF=∠BOE=90°，
∴∠OBE+∠BEO=90°，
∵AG⊥EB，
∴∠AGE=90°，
∴∠GAE+∠AEG=90°，
∴∠OBE=∠OAF，
在△AOF和△BOE中

∠AOF=∠BOE

AO=BO

∠OAF=∠OBE

∴△AOF≌△BOE（ASA），
∴OE=OF．

（2）OE=OF仍然成立．
理由：如图（2）
正方形ABCD中，∴AO=BO，∠AOF=∠BOE=90°，
∴∠FAO+∠F=90°，
∵AG⊥EB，∴∠AGE=90°，
∴∠GAE+∠E=90°，
∴∠E=∠F，
在△AOF和△BOE中

∠AOF=∠BOE

∠E=∠F

AO=BO

∴△AOF≌△BOE（AAS），
∴OE=OF．
所以结论仍然成立．

上一篇 : 顺次连接四边形各边中点，所得的
下一篇 : 如图，正方形ABCD内接于⊙O，点E在

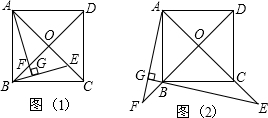
如图，正方形ABCD的对角线AC、BD相交于O．（1）（图1）若E为AC上一点，过A作AG⊥EB于G，AG、BD交于F，求证：OE=OF；（2）（图2）若E为AC延长线上一点，AG⊥EB交EB的延长线

题目简介

题目详情

答案

更多内容推荐