| (1)证明: ∵四边形ABCD、AEFG都是正方形, ∴AB=AD,AE=AG,∠BAD=∠EAG=90°, ∴∠1+∠3=90°,∠2+∠3=90°, 即∠1=∠2,∴△ADG≌△ABE;(3分) (2)∠FCN=45°,(4分) 理由如下: 过F作FH⊥MN于H,则∠EHF=90°, ∵四边形ABCD、AEFG都是正方形, ∴AB=BC,AE=EF,∠ABE=∠AEF=90°, ∴∠1+∠4=90°,∠4+∠5=90°, 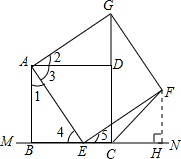 ∴∠1=∠5, 又∵∠ABE=∠EHF=90°, ∴△ABE≌△EHF,(6分) ∴BE=HF,AB=EH, ∴BC=EH, ∴HC=BE, ∴在Rt△CHF中,CH=FH, ∴∠FCN=∠CFH=45°.(8分) |
题目简介
如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,观察并猜测∠FCN的度数
题目详情
MN上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由.