 ∵正方形ABCD的边长为1, ∴AB+AD=1+1=2, ∵△APQ的周长为2, ∴AP+AQ+PQ=2, 又∵AB=AP+BP,AD=AQ+DQ, ∴DQ+BP=PQ, 将△CBP绕点C顺时针旋转90°得△CDE, 则CE=CP,DE=BP,∠BCP=∠DCE, ∴EQ=DQ+DE=DQ+BP=PQ, 在△CPQ和△CEQ中,
∴△CPQ≌△CEQ(SSS), ∴∠PCQ=∠ECQ, 又∵∠PCQ+∠ECQ=∠PCQ+∠DCQ+∠DCE=∠PCQ+∠DCQ+∠BCP=∠BCD=90°, ∴∠PCQ=
|
题目简介
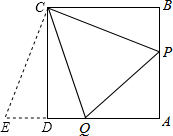
如图,正方形ABCD的边长为1,P为AB上的点,Q为AD上的点,且△APQ的周长为2.求∠PCQ的度数.-数学
题目详情