将五个边长都为2cm的正方形按0图所示摆放，点A、B、C、D分别是四个正方形的中心，（以下有（1）、（2）两问，每个考生只须选答一问，若两问都答，则只以第（2）问计分）（1）第一问：图-数学

题目简介

将五个边长都为2cm的正方形按0图所示摆放，点A、B、C、D分别是四个正方形的中心，（以下有（1）、（2）两问，每个考生只须选答一问，若两问都答，则只以第（2）问
360优课网

计分）
（1）第一问：图中△AMN的面积是______；
（2）第二问：图中四块阴影面积的和为______．

题型：填空题难度：中档来源：不详

（1）∵点A是正方形的中心，
∴点A到MN的距离等于边长的class="stub"1

，即1cm，
∴△AMN的面积=class="stub"1

×2×1=1cm2；

（2）如图，过B作分别作正方形两边的垂线，垂足分别为E、G，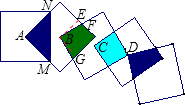
360优课网

∴∠BEF=∠BGH=90°，BE=BG=1cm，∠FBG=90°，
∵∠EBF+∠FBG=90°，∠FBG+∠GBH=90°，
∴∠EBF=∠GBH，
在△BEF与△BGH中，

∠BEF=∠BGH=90°

∠EBF=∠GBH

BE=BG

，
∴△BEF≌△BGH（AAS），
∴S△BEF=S△BGH，
∴阴影部分的面积=1×1=1cm2，
同理可证，其它阴影部分的面积都是1cm2，
∴四块阴影面积的和为：1×4=4cm2．
故答案为：（1）1cm2，4cm2．