| (1)不能为90°. 取AB、HG的中点M、N,连接MN、MH. 在△BMH中,∠BMH=135°,∠MBH+∠MHB=45°, 又 MH>MB, ∴∠MBH>∠MHB, ∴∠MBH>22.5°, ∴4∠ABH>90°, ∴按方案三所焊接而成的大扇形的圆心角必大于90°. 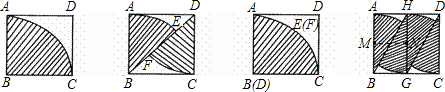 (2)不能相等,面积增大. ∵S扇形=
由于
∴圆心角θ增大,扇形的面积必增大. (3)n越大,所焊接成的大扇形的面积也越大. ∵n越大,焊接而成的大扇形的圆心角越大. |
| (1)不能为90°. 取AB、HG的中点M、N,连接MN、MH. 在△BMH中,∠BMH=135°,∠MBH+∠MHB=45°, 又 MH>MB, ∴∠MBH>∠MHB, ∴∠MBH>22.5°, ∴4∠ABH>90°, ∴按方案三所焊接而成的大扇形的圆心角必大于90°.  (2)不能相等,面积增大. ∵S扇形=
由于
∴圆心角θ增大,扇形的面积必增大. (3)n越大,所焊接成的大扇形的面积也越大. ∵n越大,焊接而成的大扇形的圆心角越大. |
题目简介
电焊工想利用一块边长为a的正方形钢板ABCD做成一个扇形,于是设计了以下三种方案:方案一:如图1,直接从钢板上割下扇形ABC.方案二:如图2,先在钢板上沿对角线割下两个扇形,再-数学
题目详情
方案一:如图1,直接从钢板上割下扇形ABC.
方案二:如图2,先在钢板上沿对角线割下两个扇形,再焊接成一个大扇形(如图3).
方案三:如图3,先把钢板分成两个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将四个小扇形按与图3类似的方法焊接成一个大扇形.
试回答下列问题:
(1)容易得出图1、图3中所得扇形的圆心角均为90°,那么按方案三所焊接成的大扇形的圆心角也为90°吗?为什么?
(2)容易得出图1中扇形与图3中所得大扇形的面积相等,那么按方案三所焊成的大扇形的面积也与方案二所焊接成的大扇形的面积相等吗?若不相等,面积是增大还是减小?为什么?
(3)若将正方形钢板按类似图4的方式割成n个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这2n个小扇形按类似方案三的方式焊接成一个大扇形,则当n逐渐增大时,所焊接成的大扇形的面积如何变化?