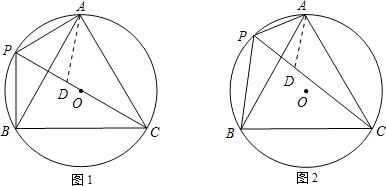 证明:(1)∵△ABC为正三角形, ∴∠APC=∠BPC=60°, ∵PC为⊙O的直径, ∴∠PAC=∠PBC=90°, ∴AP=BP=
∴AP+BP=PC; (2)成立. 在PC上取一点D,使PD=PA,连接AD; ∵∠APD=60°, ∴△APD为等边三角形, ∴AD=PD; ∵∠PAD=∠BAC=60°, ∴∠PAB=∠DAC, ∵AP=AD,AB=AC, ∴△APB≌△ADC, ∴PB=DC, ∴PA+PB=PD+DC=PC. |
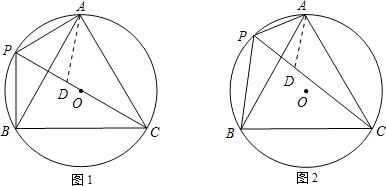 证明:(1)∵△ABC为正三角形, ∴∠APC=∠BPC=60°, ∵PC为⊙O的直径, ∴∠PAC=∠PBC=90°, ∴AP=BP=
∴AP+BP=PC; (2)成立. 在PC上取一点D,使PD=PA,连接AD; ∵∠APD=60°, ∴△APD为等边三角形, ∴AD=PD; ∵∠PAD=∠BAC=60°, ∴∠PAB=∠DAC, ∵AP=AD,AB=AC, ∴△APB≌△ADC, ∴PB=DC, ∴PA+PB=PD+DC=PC. |
题目简介
已知:⊙O是正三角形ABC的外接圆.(1)如图1,若PC为⊙O的直径,连接AP,BP,求证:AP+BP=PC;(2)如图2,若点P是弧AB上任一点,连接AP,BP,那么结论AP+BP=PC还成立吗?试
题目详情
(1)如图1,若PC为⊙O的直径,连接AP,BP,求证:AP+BP=PC;
(2)如图2,若点P是弧AB上任一点,连接AP,B
P,那么结论AP+BP=PC还成立吗?试证明你的结论.